Notes: Nassim N. Taleb's Philosopher Stone
summary from Book V, Chapter 19
- Someone with a linear payoff needs to be right more than 50 percent of the time. Someone with a convex payoff, much less. The hidden benefit of antifragility is that you can guess worse than random and still end up outperforming. Here lies the power of optionality. Your function of something is very convex, so you can be wrong and still do fine—the more uncertainty, the better.
- In summary: if you have favorable asymmetries, or positive convexity, options being a special case, then in the long run you will do reasonably well, outperforming the average in the presence of uncertainty. The more uncertainty, the more role for optionality to kick in, and the more you will outperform. This property is very central to life.
- [ref. 1] This method does not require a good model for risk measurement. Take a ruler. You know it is wrong. It will not be able to measure the height of the child. But it can certainly tell you if he is growing. In fact the error you get about the rate of growth of the child is much, much smaller than the error you would get measuring his height. The same with a scale: no matter how defective, it will almost always be able to tell you if you are gaining weight, so stop blaming it. Convexity is about acceleration. The remarkable thing about measuring convexity effects to detect model errors is that even if the model used for the computation is wrong, it can tell you if an entity is fragile and by how much it is fragile. As with the defective scale, we are only looking for second-order effects.
The Philosopher’s stone
The three main elements:
- (a) The severity of the problem of conflation (mistaking the price of oil for geopolitics, or mistaking a profitable bet for good forecasting—not convexity of payoff and optionality).
- (b) Why anything with optionality has a long-term advantage—and how to measure it.
- (c) An additional subtle property called Jensen’s inequality.
A toy example: The number of cars is the variable; traffic time is the function of the variable. The behavior of the function is “not the same thing”. We can see here that the function becomes different from the variable under nonlinearities.
- (a) The more nonlinear, the more the function divorces itself from the variable. If traffic were linear, then there would be no difference in traffic time between the two following situations: 90,000, then 110,000 cars on the one hand, or 100,000 cars on the other.
- (b) The more volatile the variable, the more the function divorces itself from the variable. Let us consider the average number of cars again. The function (travel time) depends more on the volatility around the average. Things degrade if there is unevenness of distribution. For the same average you prefer to have 100,000 cars for both time periods; 80,000 then 120,000, would be even worse than 90,000 and 110,000.
- (c) If the function is convex (antifragile), then the average of the function is going to be higher than the function of the average of each variable. And the reverse when the function is concave (fragile).
Examples
Convex Example:
- As an example for (c), which is a more complicated version of the bias, assume that the function under question is the squaring function (multiply a number by itself). This is a convex function. Take a conventional die (six sides) and consider a payoff equal to the number it lands on, that is, you get paid a number equivalent to what the die shows—1 if it lands on 1, 2 if it lands on 2, up to 6 if it lands on 6. The square of the expected (average) payoff is then \((\frac{1+2+3+4+5+6}{6})^2\), equals \(3.5^2\), here 12.25. So the function of the average equals 12.25.
- But the average of the function is as follows. Take the square of every payoff, \(\frac{1^2+2^2+3^2+4^2+5^2+6^2}{6}\), that is, the average square payoff, and you can see that the average of the function equals 15.17.
- So, since squaring is a convex function, the average of the square payoff is higher than the square of the average payoff. The difference here between 15.17 and 12.25 is what I call the hidden benefit of antifragility—here, a 19 percent “edge.”
Concave Example:
- The square root of the expected (average) payoff is then \(\frac{\sqrt{1+2+3+4+5+6}}{6}\), equals \(\sqrt{3.5}\), here 1.87. The function of the average equals 1.87.
- But the average of the function is as follows. Take the square root of every payoff, \(\frac{\sqrt{1}+\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{5}+\sqrt{6}}{6}\), that is, the average square root payoff, and you can see that the average of the function equals 1.80.
Modelling Second Order Effects and Fragility
summary from the appendix II
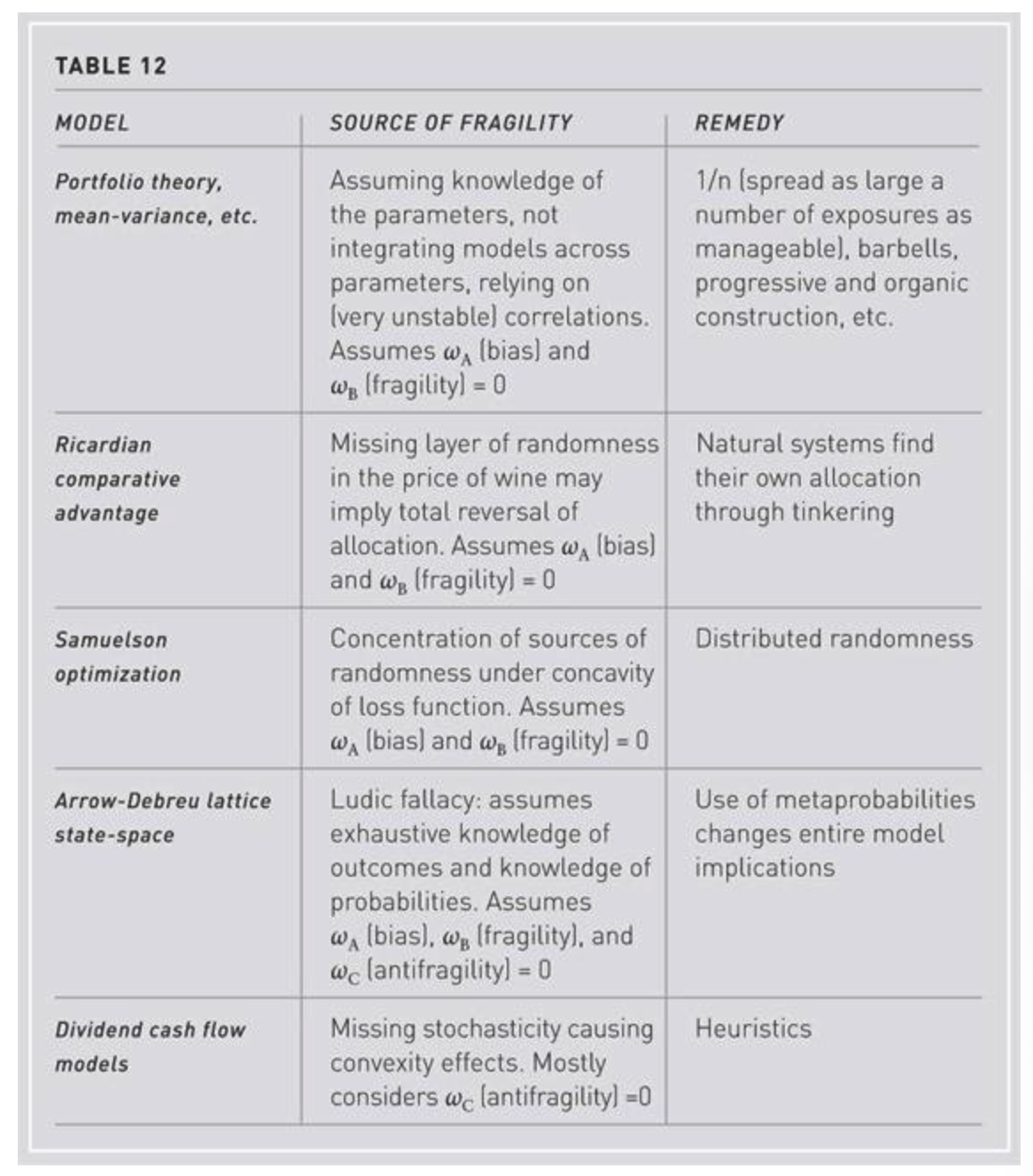
Assume we have the right model (which is a very generous assumption) but are uncertain about the parameters.
As a generalization of the deficit/employment example used in the previous section:
say we are using, a simple function: \(f(x \mid \bar{\alpha} )\) where \(\bar{\alpha}\) is supposed to be the average expected input variable, where we take \(\varphi\) as the distribution of \(a\) over the domain \(D_{\alpha}\) is:
\[\int_{D_a}{ \alpha \varphi(\alpha) d\alpha}\]The philosopher’s stone:
The mere fact that \(\alpha\) is uncertain (since it is estimated) might lead to a bias if we perturbate from the inside (of the integral), i.e., stochasticize the parameter deemed fixed. Accordingly, the convexity bias is easily measured as the difference between (a) the function \(f\) integrated across values of potential \(\alpha\), and (b) \(f\) estimated for a single value of α deemed to be its average. The convexity bias (philosopher’s stone) \(\omega_{A}\) becomes (see [ref. 1]):
\[\omega_{A} = \int_{D_x}\int_{D_\alpha} f(x \mid \alpha) \varphi(\alpha) d\alpha \ dx - \int_{D_x}f(x \mid (\int_{D_\alpha} \alpha \varphi(\alpha) d\alpha))dx\]The central equation: Fragility is a partial philosopher’s stone below \(K\), hence \(\omega_{B}\) the missed fragility is assessed by comparing the two integrals below \(K\) in order to capture the effect on the left tail:
\[\omega_{B}(K) = \int_{-\infty}^{K}\int_{D_\alpha} f(x \mid \alpha) \varphi(\alpha) d\alpha dx - \int_{-\infty}^Kf(x \mid (\int_{D_\alpha} \alpha \varphi(\alpha) d\alpha))dx\]which can be approximated by an interpolated estimate obtained with two values of \(\alpha\) separated from a midpoint by \(\Delta\alpha\)$ its mean deviation of α and estimating:
\[\omega_{B}(K) = \int_{-\infty}^{K} \frac{1}{2}( f(x \mid \bar{a} + \Delta\alpha) + f(x \mid \bar{a} - \Delta\alpha))dx - \int_{-\infty}^K f(x \mid \bar{\alpha})dx\]Note that antifragility \(\omega_{C}\) is integrating from \(K\) to \(\infty\). We can probe \(\omega_{B}\) by point estimates of \(f\) at a level of \(X ≤ K\)
\[\omega_{B}'(K) = \frac{1}{2}( f(X \mid \bar{a} + \Delta\alpha) + f(x \mid \bar{a} - \Delta\alpha) )dx - f(X \mid \bar{\alpha})\]so that:
\[\omega_{B}(K) = \int_{-\infty}^{K}\omega_{B}'(K)dx\]which leads us to the fragility detection heuristic (Taleb, Canetti, et al., 2012). In particular, if we assume that \(\omega_{B}'(X)\) has a constant sign for \(X ≤ K\), then \(\omega_{B}(K)\) has the same sign. The detection heuristic is a perturbation in the tails to probe fragility, by checking the function \(\omega_{B}'(X)\) at any level \(X\).